bípedos implumes

UN PDF MUY INTERESANTE QUE COMPLETA EL TEMA Y QUE NO RECUERDO DE DÓNDE BAJÉ, DESDE AQUÍ MI AGRADECIMIENTO DESMEMORIADO AL AUTOR O AUTORA. MUCHAS GRACIAS!

 

1. INTRODUCCIÓN

El lenguaje es un medio de comunicación humano. El estudiarlo desde el punto de vista filosófico tiene su justificación en el hecho de que uno de los temas principales de la filosofía es el llegar a entender cómo conocemos, hasta dónde podemos conocer, hasta qué punto nuestro conocimiento es verdadero o no lo es, etc... Y como todo conocimiento se expresa mediante el lenguaje, la filosofía debe ocuparse de él.

El lenguaje puede ser estudiado desde tres puntos de vista.

a) Sintáctico: Estudia el modo en que se relacionan las palabras entre sí. Su principal interés reside en la forma, es decir, en si una proposición está bien construída:

• Mal: “La vida son necesarios y el sol para el agua” / Bien: ”El sol y el agua son necesarios para la vida”

b) Semántico: Estudia el significado de las palabras y oraciones. Su principal interés reside en el contenido:

• “Pienso, luego existo” / “La fe es una gracia divina”

c) Pragmático: Estudia el modo en que un grupo humano o un individuo determinado utilizan el lenguaje. Su principal interés es el contexto y la intención de los hablantes al decir algo:

• “El vino de Ocaña !Buenísimo¡“ / “Él vino de Ocaña buenísimo”

Dicho todo lo anterior, la lógica se centra en el aspecto sintáctico o formal, dejando de lado el contenido. No se ocupa de que el discurso tenga sentido, sino sólo si está bien construido.

La lógica es una disciplina filosófica muy antigua, casi tanto como la propia filosofía (Siglo VI-V a.C.). Fue Parménides de Elea quien formuló por primera vez uno de los principios fundamentales de la lógica: El Principio de no contradicción ¬(A ⋀¬A). Aunque el principio no estaba aún formalizado, lo enunció así: “Sólo lo que es, es, y lo que no es, no es, y no puede ser pensado”. Pero fue Aristóteles en el siglo IV a.C. quien por primera vez sistematiza la lógica a través de lo que él llamó “silogística”. El silogismo es un razonamiento que consta de tres proposiciones, dos de las cuales son premisas (Mayor y Menor) y una, la última, es la conclusión:

Todos los hombres son mortales --->la mayor

Sócrates es hombre --->la menor

Sócrates es mortal -->Conclusión

A finales del siglo XIX y primeros del XX, dado el auge y la complejidad que fueron adquiriendo las ciencias: física y matemáticas, surgió la necesidad de lo que hoy llamamos Lógica matemática, con el fin de comprobar a través de lo que se llama cálculo proposicional o cuantificacional la corrección o incorrección formal de los enunciados científicos, especialmente los matemáticos y los físicos. Hoy en día la lógica se emplea en lo que hemos dicho, pero tiene su principal aplicación en el campo de la informática.

 

2. DEFINICIÓN

A) ¿QUÉ ES LA LÓGICA?:

La ciencia que estudia las leyes del razonamiento correcto o formalmente válido. El razonamiento correcto es el resultado de partir de ciertos datos que conocemos previamente: premisas (P) , de las que se van derivando o siguiendo (deduciendo) conclusiones(C). Si las premisas son verdaderas, entonces la conclusión también lo será. Los enunciados: premisas y conclusión, pueden ser verdaderos o falsos. En cambio, los razonamientos no son ni verdaderos ni falsos, sino correctos o incorrectos.

P1- Todos los hombres son mortales

P2- Sócrates es hombre

C ⊣ Sócrates es mortal

P1- Todos los hombres son mortales

P2- Pedro es hombre

C ⊣ Pedro es inteligente

Aunque Pedro sea en realidad un completo idiota, el argumento es correcto, porque partimos de ciertas premisas que damos por válidas (en lógica nos interesa la forma de los razonamientos, no el contenido)

 

b) ¿QUÉ ES LA LÓGICA PROPOSICIONAL?

Es la lógica que se ocupa de las proposiciones y de averiguar si un enunciado (oración) es formalmente válido o no lo es. Como ya hemos señalado, estudia también las relaciones que existen entre diversos enunciados: premisas y conclusiones.

 

c) ¿QUÉ ES UNA PROPOSICIÓN?

Es una oración enunciativa, la cual afirma o niega algo:

• • “Sócrates es filósofo” / “Sócrates pasea y Platón habla sin parar”
• Pero no todas las oraciones son proposiciones, por ej.:
• • “¡Ojalá termine pronto el curso!
• • “¡Vete a hacer gárgaras!”

Estas oraciones son, respectivamente, oraciones desiderativa e imperativa.

En gramática podemos analizar los enunciados estableciendo sujeto y predicado. En cambio, en lógica se analizan como un todo, distinguiendo el número de sujetos al que afecta la predicación. Lo veremos más claro en los tipos de proposición.

Las proposiciones atómicas son las que no pueden descomponerse en partes que a su vez sean proposiciones, generalmente tienen un sólo sujeto. Por ejemplo: "Sócrates es mortal" es atómica porque no puede descomponerse en partes que a su vez sean proposiciones, ya que decir Sócrates o mortal ni afirman ni niegan nada, simplemente nombran a un sujeto o a un predicado.

Las proposiciones moleculares son aquellas que sí se pueden descomponer en partes. Éstas se clasifican según el número de sujetos, y se caracterizan por ir conectadas por lo que llamamos conectivas del tipo: y, ó, o bien... o bien, si..., entonces, si y solo si, también, tampoco...

• • Sócrates es mortal y Platón era su discípulo.
• • Sócrates o Platón crearon la Academia.
• • Si Sócrates fue maestro de Platón, (entonces) Platón recibió la influencia socrática. •Solo si Sócrates fue maestro de Platón, Platón recibió la influencia socrática.

 

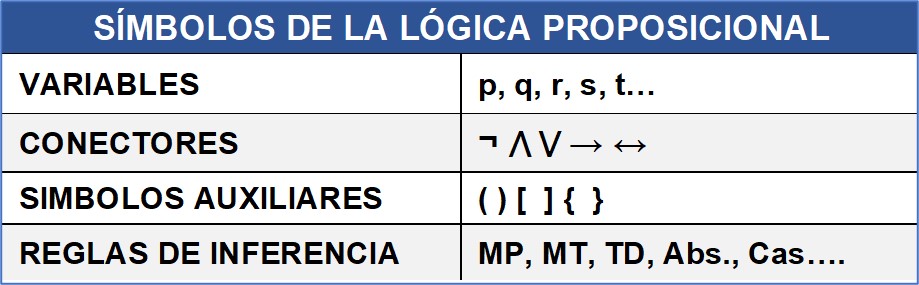
3. SÍMBOLOS DE LA LÓGICA PROPOSICIONAL

El lenguaje de la lógica se expresa simbólicamente a través de diferentes recursos:

a) Las VARIABLES son letras minúsculas enunciativas que simbolizan proposiciones p, q, r, s....

Pongamos por caso, la proposición “Sócrates es mortal” se simbolizaría con una sola letra, por ejemplo, la “p”. igual ocurriría con la proposición atómica “La Tierra es redonda” = “p”.

b) Los CONECTORES son los símbolos que se usan para enlazar diferentes proposiciones entre sí. Ej.:

• Sócrates no es ciclista = ¬p

• Fernando e Isabel fueron reyes = p ⋀ q

• El asesino puede ser Juan o Pedro = p ⋁ q

• Si llueve, (entonces) se moja el suelo = p →q

• Sólo si llueve, se moja el suelo = p ↔ q

 

c) Los signos auxiliares se utilizan para distinguir y separar proposiciones moleculares que se relacionan entre sí (del mismo modo que en matemáticas). Ej.:

Si salgo esta noche (p), no puedo estudiar (¬ q), y si no puedo estudiar ( ¬q ), no aprobaré (¬ r) . Por lo tanto, voy a estudiar ( q)

Formalizado en su totalidad sería: [(p →¬ q) ⋀ (¬q → ¬r)] → q

 

d) FORMALIZACIÓN:

Consiste en traducir las oraciones enunciativas del lenguaje ordinario (natural) al lenguaje formal (lógico) mediante la utilización de variables, conectores y demás signos lógicos.

Primero analizamos si se trata de un enunciado atómico o molecular.

Luego, seguimos analizando cómo se conectan entre sí simbolizándolo con la conectiva correcta, y empleando, si es necesario, signos auxiliares.

Ejercicios de formalización:

• 1. La lógica es la ciencia del razonamiento correcto.
• 2. El diamante es una piedra preciosa
• 3. El diamante y el carbón tienen como principal componente el carbono.
• 4. En Extremadura, como su propio nombre indica, el tiempo es muy bueno o muy malo.
• 5. No es cierto que los cerezos florezcan en invierno.
• 6. Si se cae la viga maestra, se cae toda la casa.
• 7. Si no se cae la viga maestra, no se cae toda la casa.
• 8. Si llueve y se abona bien la tierra, las plantas crecen más frondosas.
• 9. Si los partidos liberales ganan las elecciones, pueden ocurrir dos cosas: o bien mejora la economía, o bien empeoran las condiciones de trabajo de los obreros. Si mejora la economía, aumentará el consumo, pero también disminuirá el ahorro y aumentará la inflación.

 

4. TABLAS DE VERDAD

Son un instrumento para averiguar si un enunciado, o un conjunto de enunciados, es o son formalmente válidos o no.

A continuación, estudiaremos los valores de verdad y falsedad de los principales conectores lógicos:

 

 

b) CONSTRUCCIÓN DE LAS TABLAS DE VERDAD

el número de variables (p, q, r,…) nos dará el número de líneas de la tabla.

 

 

• Si en un argumento hay 2 variables distintas, aplicaremos 2 elevado a 2 = 4 filas.

• Si en un argumento hay 3 variables distintas, aplicaremos 2 elevado a 3 = 8 filas.

• Si en un argumento hay 4 variables distintas, aplicaremos 2 elevado a 4 = 16 filas.

• Si en un argumento hay 5 variables distintas, aplicaremos 2 elevado a 5 = 32 filas….

El orden en que pondremos en las columnas los valores será el siguiente:

• En caso de que haya dos variables: p, q. A la primera p variable le asignaremos en su columna correlativamente 1,1 y 0,0 A la segunda q le asignaremos en su columna de forma alterna 1,0, 1,0

• En caso de que haya tres variables: p, q ,r. A la primera p variable le asignaremos en su columna correlativamente 1,1,1,1 y 0,0,0,0 A la segunda q le asignaremos:1, 1, 0,0,1,1, 0,0 A la tercera r: 1,0,1,0,1,0,1,0

• En caso de que haya cuatro variables: p, q, r, s. A la primera variable p le asignaremos en su columna correlativamente 1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0, A la segunda q le asignaremos en su columna de forma alterna 1,1,1,1,0,0,0,0, 1,1,1,1, 0,0,0,0 A la tercera r: 1,1,0,0,1,1,0,0,1,1,0,0,1,1,0,0 A la cuarta s: 1,0,1,0,1,0,1,0, 1,0,1,0,1,0,1,0 En caso de que alguna variable esté negada, comenzaremos asignando en la columna que le corresponda un orden inverso: colocaremos primero con los valores negativos: 0 con la alternancia que corresponda según el número de variables y su lugar en el argumento. Ejemplo:

 

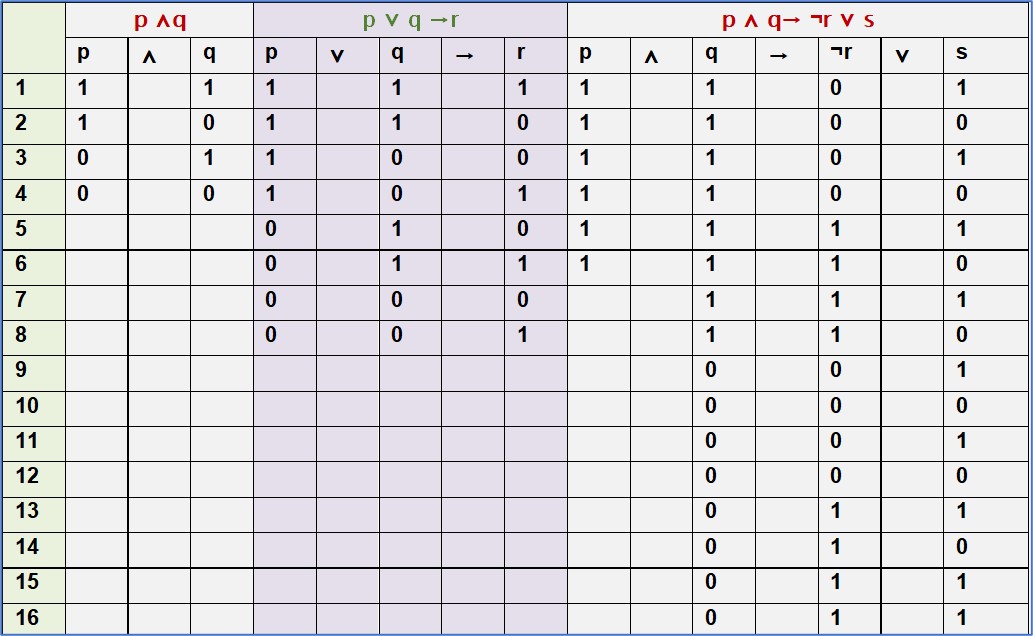
Pongamos un ejemplo con dos argumentos:

 

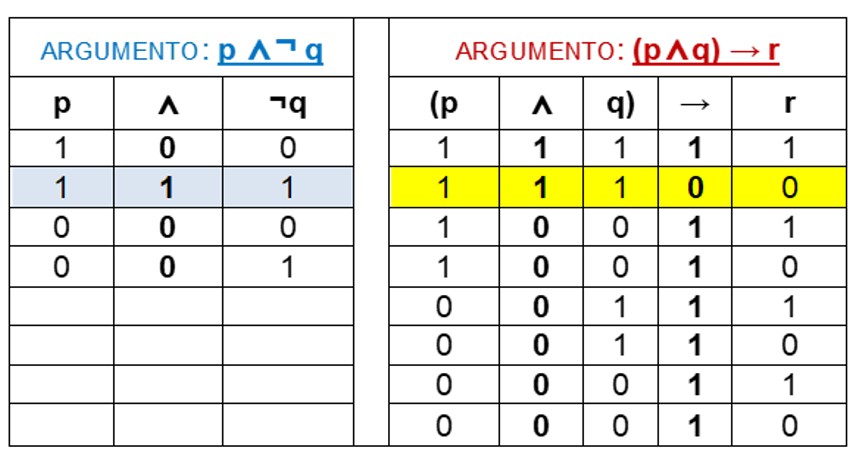
Pongamos un ejemplo del proceso: Dado el siguiente argumento: [(p⋀q)→¬r)]⋀(r→s)

Lo primero que debemos tener en cuenta, después de calcular el número de líneas escribiendo los correspondientes valores de verdad (1) y falsedad (0) en la columna correspondiente de cada variable, será:

Establecer cuál es el conector principal, que se analizará en último lugar. Distinguiremos el número de enunciados con ese fin, el conector que los enlace a todos será el principal. En este caso es el conjuntor que relaciona los dos argumentos.

A continuación, analizaremos las relaciones que se establecen entre las variables en orden creciente, es decir: iremos dando valores a los conectores menos importantes y terminaremos con el principal. Será éste el que determine el valor de verdad o falsedad de toda la tabla:

 

 

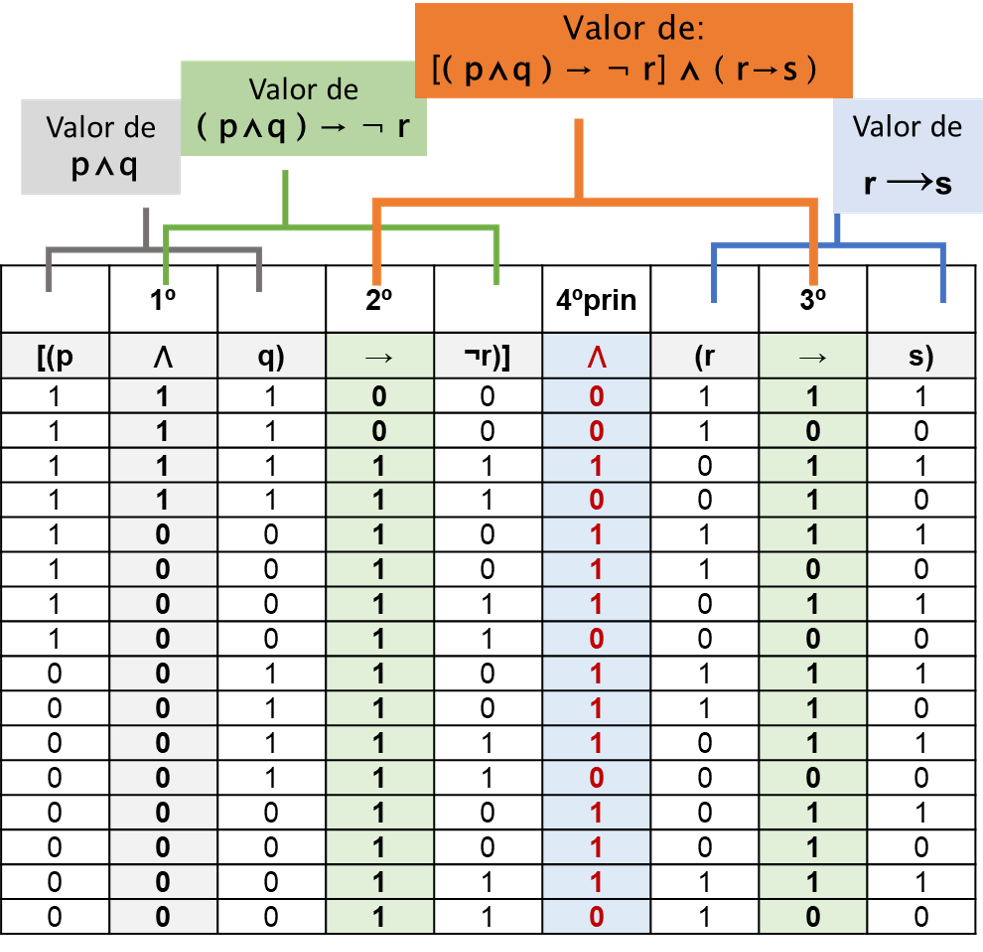
A partir del análisis del conector principal de un argumento podemos saber el grado de verdad o falsedad de dicho argumento.

• Si todos los valores son verdaderos, decimos que se trata de una TAUTOLOGÍA: una ley de lógica, siempre verdadera.

• Si, por el contrario, todos los valores son falsos, decimos que se trata de una CONTRADICCIÓN.

• Por último, si se alternan valores de verdad y falsedad, decimos que se trata de un argumento CONTINGENTE o INDETERMINADO.

Ejercicios sobre tablas de verdad:

1. (p ⋀q) → ¬ (¬ p ⋁ ¬ q)

2. (p ⋁q) →r

3. ¬ (p ⋁ q) → ¬p → q

4. [ (p →q) ⋀ (q →r)]→ (p →r)

5. p → (q ⋁s)

6. ¬ [ (p→ q) ⋀ p] → q

7. p ⋁ q → p →q

8. [ (p → q) ⋀ (q →r)] →¬ (p → r)

9. p⋀ q → p ⋁ q

Ejercicios de formalización para repasar:

1. Si no me presento al examen de lógica, me suspenderán. Si me presento, tendré que copiar o fingir que me pongo enfermo. Pero soy incapaz de hacer alguna de esas dos cosas. Luego, me suspenderán.

2. Si te quiere, te enviará flores y te invitará a salir. Sin embargo, ni te envía flores ni te invita a salir. Sintiéndolo mucho: no te quiere.

3. A Sicilia se puede ir o bien por aire o bien por mar. Si elegimos el avión, aterrizaremos en el aeropuerto de Sicilia. Si hacemos el viaje en barco, arribaremos al puerto siciliano. Tanto por barco, como por avión hemos llegado a Sicilia, así pues, queda demostrado que ambos medios de transporte son adecuados.

 

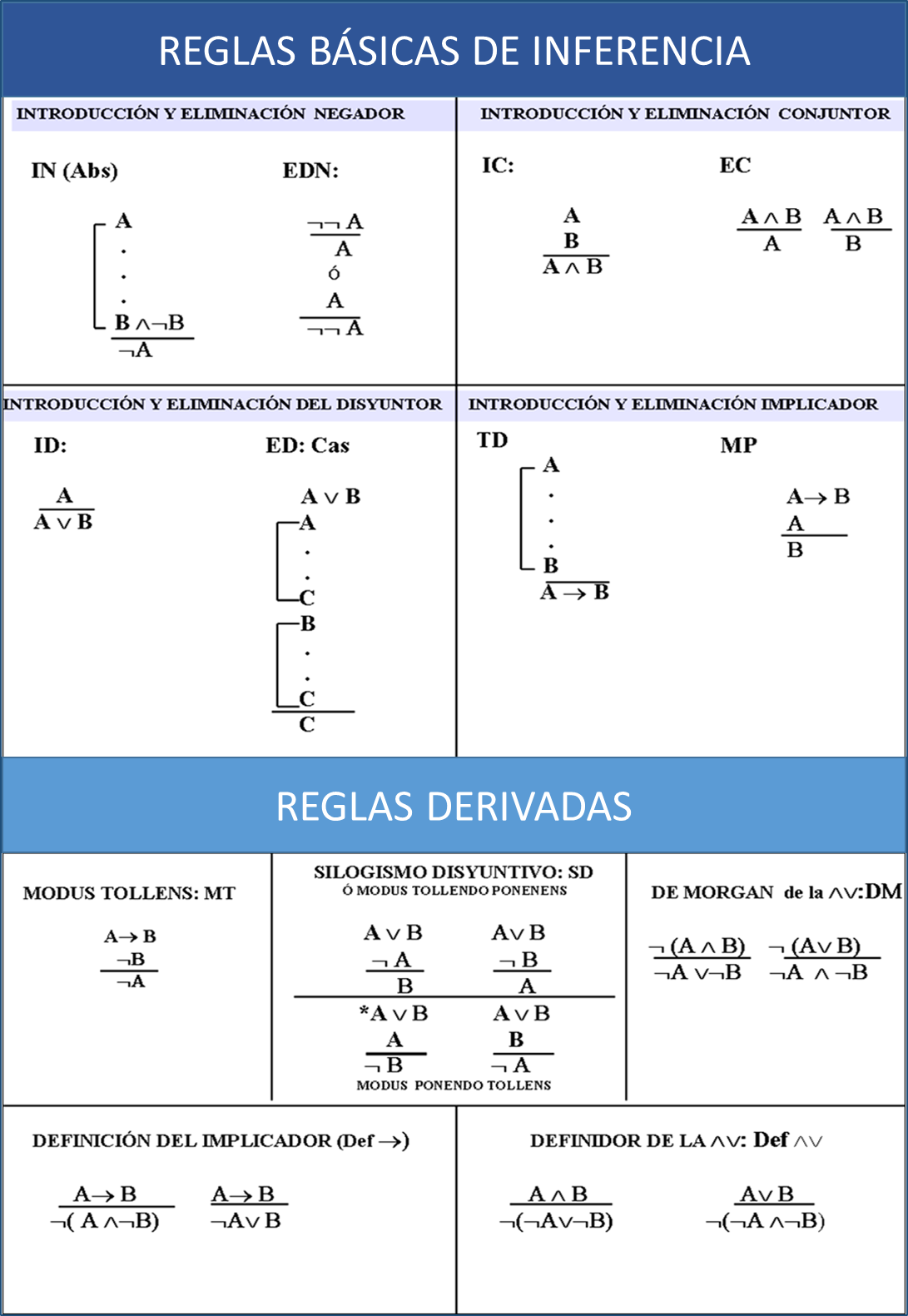
5. REGLAS BÁSICAS DE INFERENCIA

Las reglas básicas del cálculo de juntores nos sirven para comprobar la validez o no de los razonamientos, al igual que las tablas de verdad. Pero cuando un razonamiento consta de muchas premisas o de muchas variables diferentes, el procedimiento de las tablas de verdad se hace muy laborioso, y, por tanto, utilizaremos las reglas del cálculo para deducir su validez o invalidez.

Una regla de inferencia es una norma que establece un modo válido de realizar un cálculo pasando de unas proposiciones a otras según ciertas reglas. Explica, en definitiva, cómo debemos proceder. Una de las reglas elementales es por ejemplo el llamado Modus Ponens (MP):

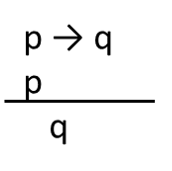
Un esquema de inferencia es la expresión formal de una regla de inferencia. Toda regla puede esquematizarse en un esquema o forma de razonamiento. Siguiendo el ejemplo del MP:

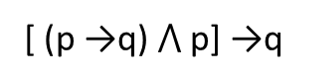
Las reglas de inferencia nos servirán para deducir conclusiones (son el resultado final de la deducción) partiendo de ciertas premisas (son las hipótesis de las que partimos), éstas se distinguen de las otras proposiciones dentro del cálculo porque las precede un guion:

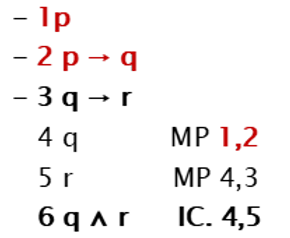
Colocamos a la derecha las reglas que estamos aplicando, especificando los números de línea. Ejemplo: en el MP de la línea 4, aclaramos que hemos hallado el antecedente p en la línea 1 y lo hemos aplicado sobre la línea 2 en la que hemos encontrado la implicación de la q es el consecuente.

 

5. PRINCIPALES REGLAS DE INFERENCIA

A) INTRODUCCIÓN Y ELIMINACIÓN DEL NEGADOR: IN O ABSURDO (ABS):

REGLA: si de una premisa “A” se llega a una contradicción, cancelaremos la premisa y concluiremos que “A” es falsa, y por lo tanto, la negaremos.

Esta regla se emplea cuando no existe otro modo de llegar a la conclusión. Para aplicarla suponemos lo contrario de lo que nos piden en la conclusión --> si nos piden "A", supondremos "¬A", si nos piden "¬A", supondremos "A" y aplicando otras reglas de inferencia deberemos llegar a la afirmación y la negación en conjunción de una proposición distinta de la que partimos (en este caso "B y noB")

En el lenguaje natural encontramos ejemplos notables de este procedimiento. Sócrates y los sofistas practicaron mucho este tipo de argumentos. Para ilustrar el arte mayeútica de Sócrates y su habilidad para reducir al absurdo la argumentación de su adversario, trascribo a continuación una escena de la película “Sócrates” del director italiano Roberto Rossellini en 1971:

- Te saludo Sócrates.

– i oh, excelente Hipias! Hace mucho que no teníamos el placer de verte en la ciudad. ¿A dónde vas tan bien equipado?

- Al gimnasio a pronunciar un discurso sobre la genealogía de los dioses ¿Te gustaría escucharlo?

- Tengo cosas que hacer y lamentablemente no puedo acompañarte.

- Es un discurso que ya he hecho, todos nos han dicho que es muy bello. Sería un placer tener también tu opinión.

- ¿Dijiste muy bello? ¿Sabes entonces qué es la belleza?

- Claro, ciertamente.

- ¿Y serías capaz de explicarlo?

- Nada más fácil, una bella virgen, he ahí Sócrates lo que es bello.

- Buena respuesta, pero dime Hipias ¿Se podría decir que una mula es bella?

- En mi pueblo hay mulas de gran belleza.

- ¿Y una cacerola se puede decir que es bella?

- No entiendo querido Sócrates que te puedas servir de un objeto tan prosaico para hablar de cosas tan elevadas.

- Es que soy tan rústico, De todos modos, aún tú debes aceptar que una cacerola es bella.

- Si, quizás, pero la más bella cacerola en comparación con una bella virgen es fea. Como la más bella de las vírgenes será fea en comparación con un dios ¿No es eso lo que quieres decir?

- Exactamente

- Y, sin embargo, antes dijiste: una bella virgen, he aquí lo que es bello. Y ahora dices que comparado con un dios es fea. Pero no puede ser bella y fea al mismo tiempo.

- Te lo explicaré otro día, cuando quieras. Te saludo Sócrates.

 

ELIMINACIÓN E INTRODUCCIÓN DE LA DOBLE NEGACIÓN (EN):

REGLA: de una premisa “A” podemos concluir su doble negación y viceversa.

La emplearemos cuando necesitemos eliminar una doble negación. Es equivalente a la de la introducción de la doble negación (iDN) y la la emplearemos cuando necesitemos formar una doble negación.

Ejemplo en lenguaje natural: “No es verdad que no quiera aprobar lógica” equivale a “Quiero aprobar lógica”, y viceversa.

 

B) INTRODUCCIÓN Y ELIMINACIÓN DEL CONJUNTOR:

B.1) INTRODUCCIÓN DEL CONJUNTOR ( IC)

REGLA: de dos proposiciones “A” o “B” tomadas como premisa, puede concluirse la conjunción de ambas.

La emplearemos para obtener una conjunción, pero sólo podremos hacerlo si las dos proposiciones están separadas y solas en alguna línea de las premisas o la deducción.

Ejemplo en lenguaje natural:

A: Ana está en el parque.

B: Boris está en el parque.

A ⋀ B: Ana y Boris están en el parque.

 

B.2) ELIMINACIÓN DEL CONJUNTOR (EC)

REGLA: de una conjunción puede concluirse cualquiera de las dos proposiciones.

La emplearemos para separar alguno de los miembros de la conjunción siempre que queramos.

Ejemplo en lenguaje natural:

A ⋀ B: Ana y Boris están en el parque.

A: Ana está en el parque.

A ⋀ B: Ana y Boris están en el parque.

B: Boris está en el parque.

 

C) INTRODUCCIÓN Y ELIMINACIÓN DEL DISYUNTOR

C.1) INTRODUCCIÓN DEL DISYUNTOR (ID).

REGLA: dada cualquier proposición puede concluirse la disyunción con cualquier otra proposición.

Es una regla muy útil cuando necesitamos formar una disyunción en la conclusión o en cualquiera de las líneas de la deducción para obtener de ella una fórmula que nos permita aplicar alguna otra regla.

Ejemplo en lenguaje natural:

1. A: Tus síntomas son causa de un resfriado.

A ⋁ B: Tus síntomas pueden ser causa de una alergia un resfriado o de una alergia.

2. B: Tus síntomas son causa de una alergia.

B ⋁ A: Tus síntomas pueden ser causa de una alergia o un de resfriado.

 

C.2) ED. Ó PRUEBA POR CASOS (CAS.)

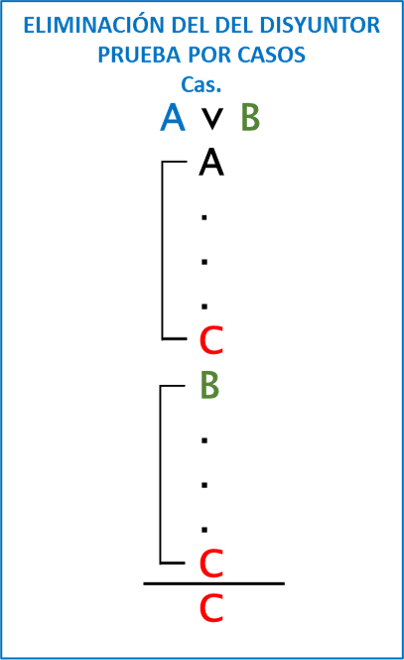
REGLA: de una disyunción A ⋁ B, demostrando que tanto el primer miembro como el segundo llegan a la misma conclusión “C” por separado, puede concluirse "C".

Se usa cuando o bien en las premisas o en alguna línea de la deducción debemos resolver una disyunción, para lo cual debemos suponer cada uno de los miembros de la disyunción y demostrar que ambos llegan a la misma conclusión, en tes caso "C".

Si alguno de los miembros de la disyunción estuviera negado en alguna parte de la deducción, no sería necesario realizar la prueba por casos. Usaríamos entonces el SD.  

Ejemplo en lenguaje natural:

1. A ⋁ B: ¿Por avión o por barco?

(A) Si vamos en avión, llegamos a Canarias. C

(B) Si vamos en barco, llegamos a Canarias. C

Conclusión: Por avión o por barco llegamos a Canarias. C

 

D) INTRODUCCIÓN Y ELIMINACIÓN DEL IMPLICADOR

D.1.) II Ó TEOREMA DE LA DEDUCCIÓN: TD:

REGLA: dada una premisa “A” si se llega a una proposición “B”, puede concluirse que A →B.

Esta regla se emplea cuando se nos pide que lleguemos a una implicación en la conclusión, para ello: suponemos el antecedente, y aplicando reglas de inferencia llegaremos al consecuente. Una vez aquí, cancelaremos el supuesto y concluiremos la implicación.

Ejemplo en lenguaje natural suponiendo otras premisas anteriores (tiene la pinta de un silogismo hipotético, epro es lo que se me ocurre en este momento:

Supuesto1. (A) Estudias de modo eficiente.

- (Si estudias de modo eficiente) te sabrás todo el tema. (C)

- Si te sabes todo el tema (C), aprobarás (B)

Conclusión: Si estudias de modo eficiente, aprobarás. A → B

 

D.2) EI MODUS PONENDO PONENS (MP)

REGLA: de una fórmula condicional y de la afirmación de su antecedente, puede concluirse la afirmación del consecuente.

Esta regla se emplea cuando necesitamos separar el consecuente (B). Sólo podremos hacerlo si encontramos suelto el antecedente (A).

Ejemplo en lenguaje natural:

A → B Si estudias, aprobarás.

A Has estudiado.

B Entonces, aprobarás.

 

E) OTRAS REGLAS DERIVADAS:

MODUS TOLLENDO TOLLENS: (MT)

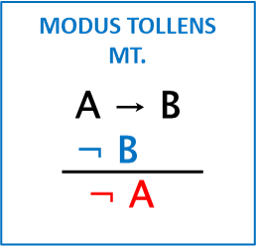
REGLA: De una fórmula condicional y la negación de su consecuente ¬ B, puede concluirse la negación del antecedente¬ A.

Sólo podremos aplicarla si encontramos suelto el consecuente negado¬ B.

Ejemplo en lenguaje natural:

A → B Si estudias, aprobarás.

¬ B No has aprobado.

¬ A Entonces, no has estudiado.

 

SILOGISMO DISYUNTIVO: (SD) (o MODUS TOLLENDO PONENS Y MODUS PONENDO TOLLENS)

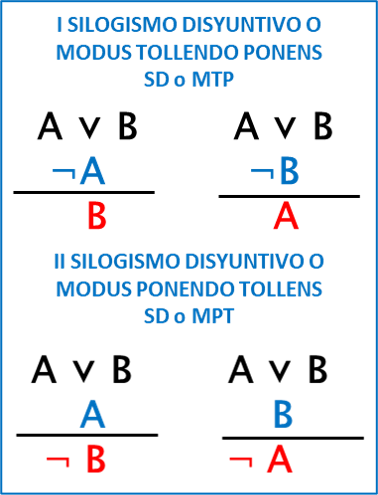
REGLA: de una disyunción y la negación de alguno de sus miembros, puede concluirse la afirmación del otro miembro.

Y de una disyunción y la afirmación de alguno de sus miembros, puede concluirse la negación del otro miembro.

Ejemplo en lenguaje natural SD I:

1. A ⋁ B Los asesinos son o Ana o Boris.

¬ A No es Ana.

B Entonces es Boris.

2. A ⋁ B Los asesinos son o Ana o Boris.

¬ B No es Boris.

A Entonces es Ana.

Ejemplo en lenguaje natural SD II:

1. A ⋁ B Los asesinos son o Ana o Boris.

A Es Ana.

¬B Entonces no es Boris.

2. A ⋁ B Los asesinos son o Ana o Boris.

B Es Boris.

¬A Entonces no es Ana.

 

DE MORGAN DE LA CONJUNCIÓN Y DE LA DISYUNCIÓN: (DM)

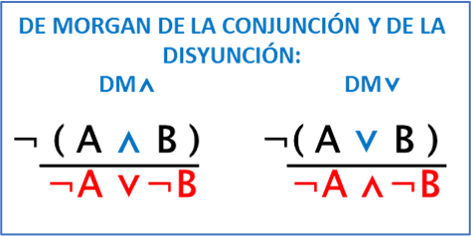
REGLA: la negación de una conjunción, o la negación de una disyunción, equivale a la negación en disyunción de cada uno de sus miembros ¬ A ⋁¬B, o la negación en conjunción de cada uno de sus miembros respectivamente: ¬A ⋀¬B

Decir: No es cierto que Ana y Boris sean asesinos ¬ ( A ⋀ B ), equivale a decir: Ana no es una asesina o Boris no es un asesino: ¬ A ⋁¬B

Decir: No es cierto que Ana o Boris sean asesinos ¬ (A ⋁ B ), equivale a decir que: Ni Ana es una asesina, ni Boris es un asesino: ¬A ⋀¬B

 

 

DEFINICIÓN DEL IMPLICADOR: (def.→)

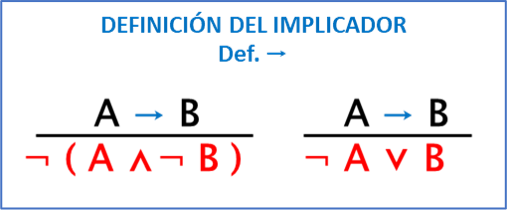
a) Decir que: si llueve, se moja el suelo equivale a decir: Que no es cierto que llueva y no se moje el suelo.

b) Decir que: Si llueve, se moja el suelo equivale a decir: Que es cierto que no llueve, o si es cierto que se moja el suelo (por causas ajenas a la lluvia) Recordemos que una implicación solo es falsa cuando el antecedente es verdadero y el consecuente es falso. Y aquí lo que se afirma es que la causa de B no es A: Un mismo efecto puede ser consecuencia de diferentes causas.

 

DEFINICIÓN DEL CONJUNTOR Y DEFINICIÓN DEL DISYUNTOR (def. ⋀ y def. ⋁ ):

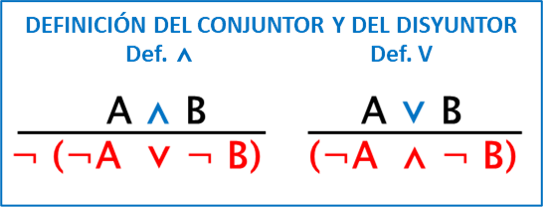
a) Decir que Ana y Boris están en el parque equivale a decir que: No es cierto que Ana esté en el parque o que Boris no esté en parque. Recordemos que el conjuntor sólo es verdadero cuando ambos términos de la conjunción son verdaderos al mismo tiempo. Si aplicamos un DM, esta equivalencia se transformará en A ⋀ B

b) Decir que Ana o Boris están en el parque equivale a decir que: No es cierto que ni Ana ni Boris están el parque. Recordemos que el disyuntor sólo es falso cuando ninguno de los miembros de la disyunción es cierto. Si aplicamos un DM, esta equivalencia se transformará en A ⋁ B